

|
Numerical examples |
|||||||
| |
||||||||
A dynamical computation of a multiple integral involved in the neutron star theoryThis study consists in computing dynamically using the CADNA library an integral involved in the neutron star theory. Massive stars collapse with an explosion ejecting all the matter, except a central residue: a neutron star or a black hole, depending on the details of the scenario. Neutron stars are mainly done of neutrons with a typical proportion of protons smaller than 10%. With time, equilibrium between protons and neutrons takes place. Time to reach this equilibrium is obtained by calculating high order integrals involving several variables for any particle appearing in the reactions.
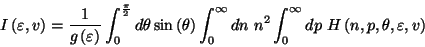
where ![$(\varepsilon,v) \in [10^{-4},10^{4}]\times[10^{-4},10^{3}]$](img2.png) and
and
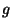 is a normalization function. is a normalization function.
with
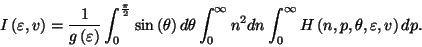
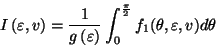
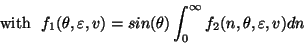
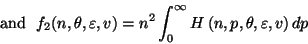
Each one-dimensional integral is evaluated by two iterative processes:
Using this strategy, the exact singificant digits of the approximation of
To get the FORTRAN source code. |